8. The VC Generators¶
This chapter gives information about the various processes that generate the so-called verification conditions, VC for short, from WhyML code.
8.1. Program Functions¶
For each program function of the form
let f (x1: t1) ... (xn: tn): t
requires { Pre }
ensures { Post }
= body
a new logic goal called f'VC is generated. Its shape is
where \(\mathit{WP}(e,Q)\) is a formula computed automatically using rules defined recursively on \(e\). The name \(\mathit{WP}\) stands for Weakest Precondition, and its computation rules are directly inspired from the original Weakest Precondition Calculus of Dijkstra. Yet, due to the particular nature of the WhyML expression language, and the underlying concept of regions to identify side effects, the computation rules for \(\mathit{WP}\) are specific to WhyML, and described in detail in a report by Filliâtre, Gondelman and Paskevich [FGP16].
8.2. Controlling the VC generation¶
The generation of VCs can be controlled by the user, in particular
using attributes put inside the WhyML source code. These attributes
are [@vc:divergent], [@vc:sp],
[@vc:wp] and
[@vc:keep_precondition]. Their effects are detailed
below.
8.2.1. Reducing size of VCs using Strongest Postconditions¶
It is known that the original form of WP calculi can possibly generate
formulas that are of exponential size in function of the size of the
corresponding program. Yet, there are known techniques to avoid this
exponential explosion [FS01]. Why3 implements its own
specific variation, which can be invoked on a per-expression basis. In
other words, this variant calculus can be activated locally on any
program expression, by putting the [@vc:sp]
attribute on that expression. Yet, the simplest usage is to pose this
attribute on the whole body of a program function.
The usage of the SP variant is in particular recommended in presence of sequence of if statements. As an example, consider the simple code below.
predicate p int
let f (x:int) (y:int) : int
ensures { p result }
= let ref r = 0 in
if 0 < x then r <- r + 1 else r <- r + 2;
if 0 < y then r <- r + 3 else r <- r + 4;
r
With the default calculus, the VC for f is
forall x:int, y:int.
if 0 < x
then forall r:int.
r = (0 + 1) ->
(if 0 < y then forall r1:int. r1 = (r + 3) -> p r1
else forall r1:int. r1 = (r + 4) -> p r1)
else forall r:int.
r = (0 + 2) ->
(if 0 < y then forall r1:int. r1 = (r + 3) -> p r1
else forall r1:int. r1 = (r + 4) -> p r1)
which contains 4 occurrences of the post-condition p r1. With
the [@vc:sp] attribute just before the line
let ref r = 0 in, the VC is now
forall x:int, y:int.
forall r:int.
(if 0 < x then r = (0 + 1) else r = (0 + 2)) ->
(forall r1:int. (if 0 < y then r1 = (r + 3) else r1 = (r + 4)) -> p r1)
which has only one occurrence of the post-condition p r1. The idea is
that the strongest post-condition of each if statement was computed
and used as an assumption for the rest of the VC.
Note that inside an expression annotated with
[@vc:sp], it is possible to switch back to the default
WP mode for a given sub-expression by annotating it with the
attribute [@vc:wp]
8.2.2. Ignoring checks for termination¶
By default, Why3 generates VCs for ensuring the termination of loops and recursive calls. For example, on the program
let f1 (x:int) : int =
let ref r = 100 in
while r > 0 do r <- r - x done;
r
Why3 issues a warning saying that the termination of the loop cannot
be proved, and the generated VC indeed contains the formula false
to prove. On the one hand, if the loop is effectively terminating, it
is expected to have a variant. On the other
hand, if a program like this is indeed intentionally not terminating,
it is expected that its contract contains the clause diverges
that makes the non-termination explicit. This exposition of potential
non-termination is propagated to callers, e.g., if continuing the same
example one writes
let f1 (x:int) : int diverges =
let ref r = 100 in
while r > 0 do r <- r - x done;
r
let g1 () = f 3
then no warning is issued for f1, and its VC does not contain
false to be proved, but the warning will be issued for
g1, and the VC for g1 contains false to be
proved. The diverges clause must be added in the contract of
g1 too.
Note that putting the diverges clause in the contract of a
function triggers an error when the function contains neither
variant-free loops nor variant-free recursive calls nor calls to
diverging functions. This behavior might be annoying for code
generators, so they can put the attribute
[@vc:divergent] on the body of the function, in
place of the diverges clause:
let f2 (x:int) : int =
[@vc:divergent]
100 - x
Note that [@vc:divergent] has the same effect as
diverges, which means that f2 is now assumed to be
diverging for functions that call it. As a consequence, the following
code will again trigger a warning about the potentially
non-terminating call to f2.
let g2 () = f2 7
8.2.3. Using a custom well-founded relation for termination¶
Variants for termination can be associated to a specific ordering
relation, thanks to the keyword with. The following example
illustrates this feature on a loop on bitvectors.
use bv.BV32
let f () =
let ref b = (42 : BV32.t) in
while BV32.sgt b (0:BV32.t) do
variant { b with BV32.slt }
b <- BV32.sub b (1:BV32.t)
done
For the termination proof to be complete, the given ordering \(r\) must be proved well-founded. In fact, it suffices to prove that, whenever proving \(r~x~y\), the term \(y\) is accessible by \(r\). The VC generator introduces a proof obligation for that.
A binary relation may be proved well-founded once and for all. In that
case, one should add the meta vc:proved_wf to the goal
proving this fact. It will prevent the VC generator to introduce any
accessibility obligation whenever this relation is used in a variant
clause. The default orderings used in variant clause (on integers,
range types, or algebraic types) are known to be well-founded by Why3,
and so are the strict ordering relations on bitvectors, as in the
example above.
8.2.4. Keeping preconditions of calls in the logical context¶
When calling a function f in a WhyML expression, a VC is
generated to check that the precondition of f holds, for the
given values of its parameters. Meanwhile, the VCs generated for the
subsequent parts of the WhyML are not explicitly given the assumption
that this precondition was valid. An example is as follows
let f (x:int) : int
requires { x > 7 }
= x-1
let g1 (y:int) =
let _ = f y in
assert { y > 0 }
On this code, after splitting the VC for g1, none of the two
subgoals generated are provable: the pre-condition of the call to
f is naturally not provable, neither is the assertion. On the
contrary, if one writes
let g2 (y:int) =
let _ = [@vc:keep_precondition] f y in
assert { y > 0 }
then the pre-condition of the call to f is known to hold after
the call, making the assertion provable.
8.3. Type Invariants¶
When a record type is given an invariant, that invariant must hold on any value of that type occurring in the considered program. It means that when a value of this type is a parameter of a function, its invariant is assumed to hold. When a value of this type is constructed in the program, a check is inserted in the VC to ensure the validity of the invariant.
Additionally, a verification condition is generated from the type
declaration itself, to ensure that the type is inhabited, that is to
ensure that there exist values for the record fields for which the
invariant holds. Proving the existence of such values might be a
difficult task for an automated prover. To help the proof of this VC,
the user can provide a witness for a possible inhabitant, using the
by keyword.
8.4. Lemma Functions¶
A useful facility to state and prove logical statements is provided by
the so-called lemma function mechanism. The principle is to add the
keyword lemma to a program function, under the following
general shape.
let lemma f (x1: t1) ... (xn: tn): unit
requires { Pre }
ensures { Post }
= body
In that case, the VC generated for f is inserted as known
logical fact in the context of the remaining goals of the considered
WhyML module.
For this to work, the function must have no side effects, be provably
terminating, and return unit. The generated fact is then
In particular, when the code of the function is recursive, it simulates a proof by induction.
8.5. Automatic Inference of Loop Invariants¶
Why3 can be executed with support for inferring loop invariants [Bau17] (see Section 4.5 for information about the compilation of Why3 with support for infer-loop).
There are two ways of enabling the inference of loop invariants: by
passing the debug flag infer:loop to Why3 or by annotating let
declarations with the [@infer] attribute.
Below is an example on how to invoke Why3 such that invariants are inferred for all the loops in the given file.
why3 ide tests/infer/incr.mlw --debug=infer:loop
In this case, the Polyhedra default domain will be used together
with the default widening value of 3. Why3 GUI will not display the
inferred invariants in the source code, but the VCs corresponding to
those invariants will be displayed and labeled with the infer-loop
keyword as shown in Fig. 8.1.
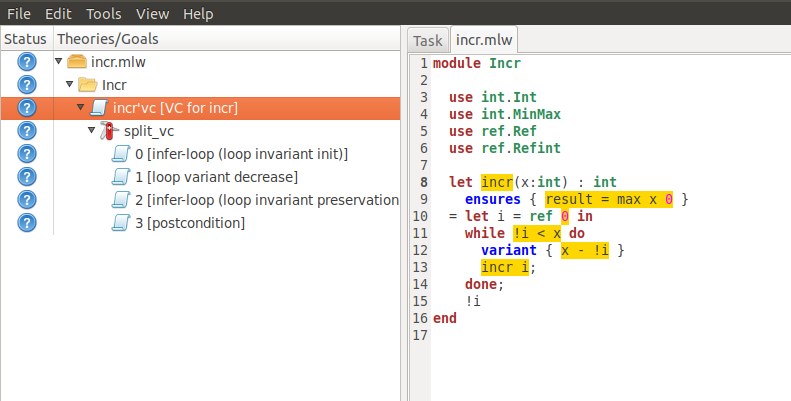
Fig. 8.1 The GUI with inferred invariants (after split).¶
Alternatively, attributes can be used in let declarations so that
invariants are inferred for all the loops in that declaration. In this
case, it is possible to select the desired domain and widening
value. In the example below, invariants will be inferred using the
Polyhedra domain and a widening value of 4. These two arguments of
the attribute can swapped, for instance, [@infer:Polyhedra:4] will
produce exactly the same invariants.
module Incr
use int.Int
use int.MinMax
use ref.Ref
use ref.Refint
let incr[@infer:4:Polyhedra](x:int) : int
ensures { result = max x 0 }
= let i = ref 0 in
while !i < x do
variant { x - !i }
incr i;
done;
!i
end
There are a few debugging flags that can be passed to Why3 to output
additional information about the inference of loop invariants. Flag
infer:print_cfg will print the Control Flow Graph (CFG) used for
abstract interpretation in a file with the name inferdbg.dot;
infer:print_ai_result will print to the standard output the
computed abstract values at each point of the CFG;
print:inferred_invs will print the inferred invariants to the
standard output (note that the displayed identifiers names might not
be consistent with those in the initial program); finally,
print:domains_loop will print for each loop the
loop expression, the domain at that point, and its translation into a
Why3 term.
8.5.1. Current limitations¶
Loop invariants can only be inferred for loops inside (non-recursive)
letdeclarations.